Introduction:

Before delving into the concept of backtracking, let's tackle some problems to gain a practical understanding of why backtracking is a valuable approach.

Prerequisites-

Before we begin, it's essential to have a basic understanding of the following concepts:

• Recursion

• Arrays

Problem Statement:

Question-1

Let's consider a scenario where a person can only move right or down in a grid, and the goal is to reach a specific cell marked in red. The question is, how many different paths can the person take to reach the red cell?

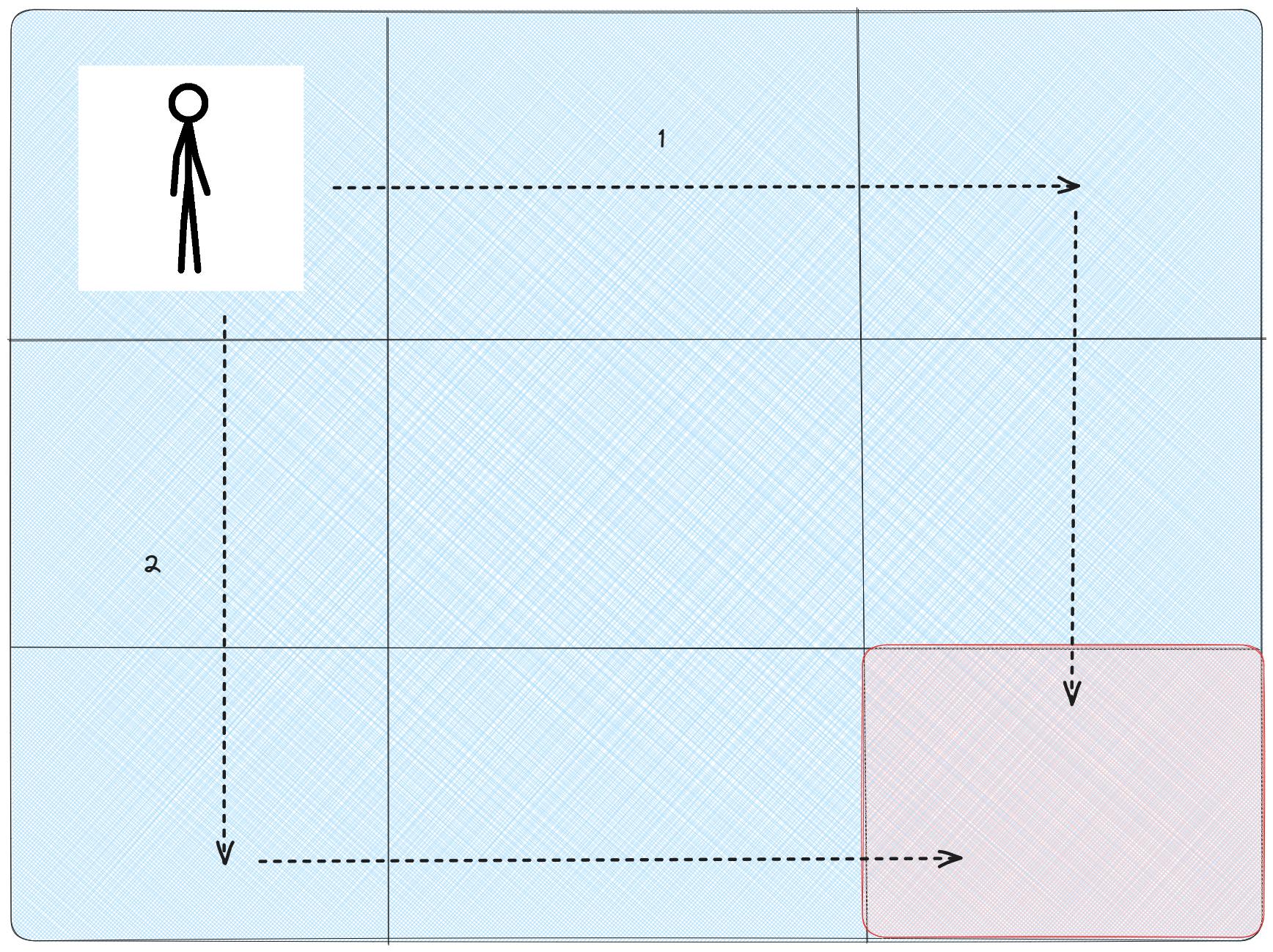
Approach:

To tackle this problem effectively, we will break it down into two main aspects:

1. What we are doing.

How we are doing it (after understanding what needs to be done)

Layman Approach

Solving this question, even for a layperson, can be approached in multiple ways. Here are some of the intuitive approaches:

1-Right-Right-Down-Down

2-Down-Down-Right-Right

3-Right-Down-Down-Right

4-Right-Down-Right-Down

Breaking Down the Problem:

Objective: Find the number of ways to reach the red cell.

Firstly, our goal is to determine how many ways it is possible to reach the red cell. To solve this problem efficiently, we will employ recursion.

Why Recursion?

The recursive approach is chosen because it can be broken down into smaller subproblems: the paths that lead to specific points and the remaining paths yet to be explored.

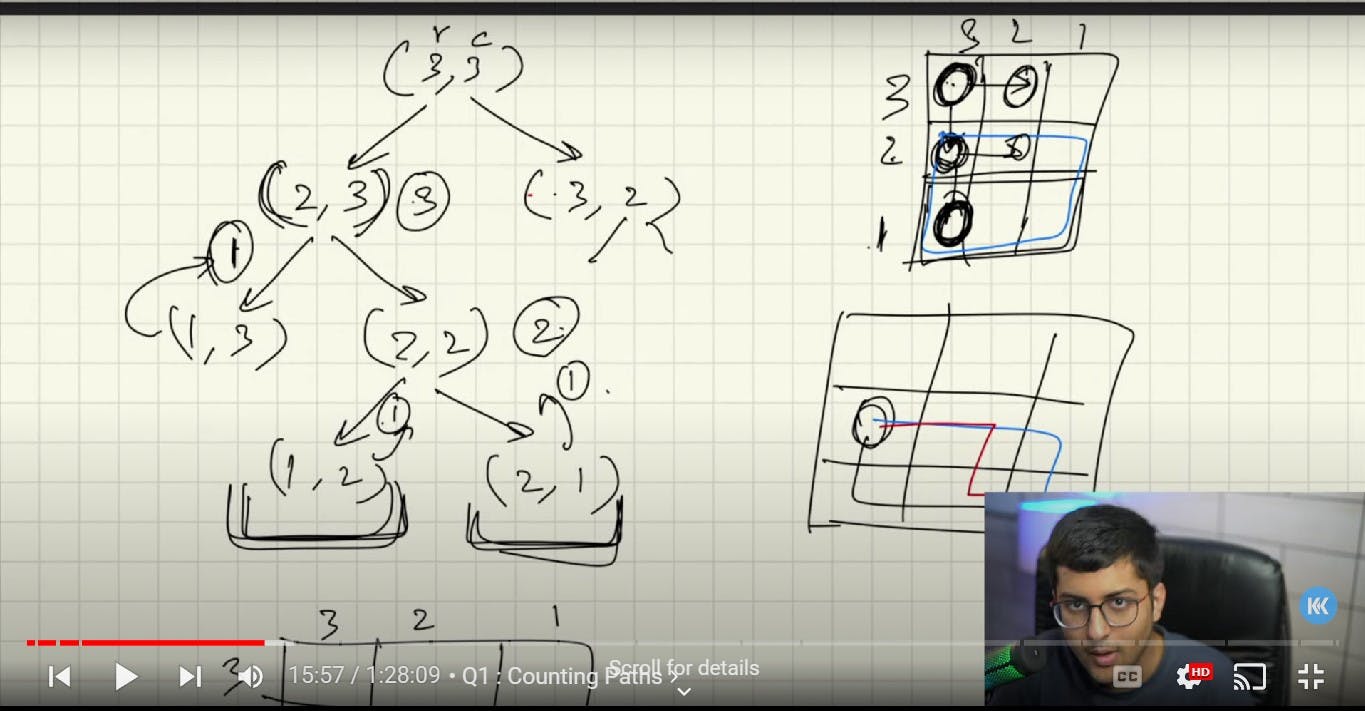
Let's Build the Recursive Tree:

Now, let's visualize the problem-solving process by constructing a recursive tree. To begin, consider the following base conditions:

1. The last column of the grid has only one way to reach the red box (by moving downward).

2. The last row of the grid also has only one way to reach the red box (by moving to the right)

[Path till that point + Remaining Paths]

Code Implementation:

To implement this approach in code, we can use Java. Below is a simple Java program that calculates the number of ways to reach the red cell in a 3x3 grid:

public class MazePrblm {
    public static void main(String[] args) {
        System.out.println(count(3, 3));
    }

    public static int count(int r, int c) {
        if (r == 1 || c == 1) {
            return 1;
        }
        int left = count(r - 1, c);
        int right = count(r, c - 1);
        return right + left;
    }
}

Output- 6

Output: The program will output the result, which in this case is 6, representing the six different ways to reach the red cell in a 3x3 grid.

Conclusion:

• Backtracking, powered by recursion, simplifies complex problems.

• It involves breaking problems into smaller subproblems.

• By exploring all possible paths, we can efficiently find solutions.

• In future notes, we'll delve deeper into advanced backtracking techniques and problem-solving scenarios.